


 Psikolog
Psikolog
 Psikolog
Psikolog
 Psikolog
Psikolog



E üssünün integrali E üssünün integrali, Kosinüs integrali nedir?, Çarpımın integrali nedir?, İntegral mantığı nedir?, İntegrali kim icat etti?, Kosinüs teoremi nasıl?
 SON YAZILAR
SON YAZILAR

Ruhsatsız Araç Kullanma Cezası 2024: Ne Kadar, Nasıl İptal Edilir?

Balat'a Nasıl Gidilir?

Rüyada Başkasının Yün Yıkadığını Görmek

İzmir'de Uzman Psikolog Bulmak: Rehber ve Fiyatlar 2024

Ankara Uzman Psikolog: Psikolog Fiyatları 2024

İstanbul Psikolog: Uzmanlık ve Fiyatlar

Hametan Krem Ne İşe Yarar?

Fucidin Krem Ne İşe Yarar?
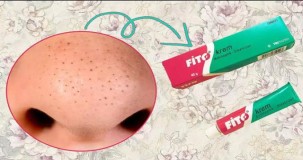
Fito Krem Ne İşe Yarar?

Rüyada Eski Sevgiliyi Görmek Ne Anlama Geliyor?

Rüyada Köpek Görmek Ne Anlama Geliyor?

Rüyada Fare Görmek Ne Anlama Geliyor?

Rüyada Hamile Olduğunu Görmek Ne Anlama Geliyor?

Rüyada Kedi Görmek Ne Anlama Geliyor?

Rüyada Deprem Olduğunu Görmek Ne Anlama Geliyor?

Rüyada Yılan Görmek Ne Anlama Geliyor?

Rüyada Altın Görmek Ne Anlama Geliyor?

Aura Ne Demek

Seküler Ne Demek

Toprak Mahsulleri Ofisi Nedir?
 POPÜLER YAZILAR
POPÜLER YAZILAR

Ruhsatsız Araç Kullanma Cezası 2024: Ne Kadar, Nasıl İptal Edilir?

Balat'a Nasıl Gidilir?

Rüyada Başkasının Yün Yıkadığını Görmek

İzmir'de Uzman Psikolog Bulmak: Rehber ve Fiyatlar 2024

Ankara Uzman Psikolog: Psikolog Fiyatları 2024

İstanbul Psikolog: Uzmanlık ve Fiyatlar

Hametan Krem Ne İşe Yarar?

Fucidin Krem Ne İşe Yarar?

Fito Krem Ne İşe Yarar?

Rüyada Eski Sevgiliyi Görmek Ne Anlama Geliyor?